Transient growth is a phenomena of convective instability in which perturbations to a fluid flow may initially show growth (although ultimately decay) as they evolve downstream, even though the flow is linearly stable. This effect is a consequence of the non-normality of the linearised Navier-Stokes operator.
Normal vs. Non-normal
A normal operator, that is one which commutes with its adjoint, has pairwise orthogonal eigenvectors. Thus, if all eigenvectors have negative eigenvalues, and consequently each eigenvector decays under the action of the operator, then any vector in the space spanned by those eigenvectors will necessarily decay.
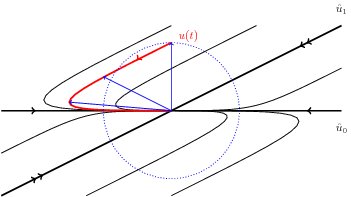
In contrast, a non-normal operator does not have pairwise orthogonal eigenvectors. This gives rise to the possibility of a vector which may initially grow in response to differing decay rates of the constituent eigenvectors. This can be seen in the diagram below. The path marked in red shows the vector initially increases in magnitude before it eventually decays.
, and Reynolds number, over all possible flow disturbances, is given by
![\[G(\tau,Re)=\max_{u_0}\frac{E(u(\tau))}{E(u(0))}\]](http://www.chriscantwell.co.uk/wp-content/ql-cache/quicklatex.com-88818c74c25265233f3ea1358a631e9e_l3.png "Rendered by QuickLaTeX.com")
Computing this numerically transforms the problem to that of finding the leading eigenvalue of 
, where 
is the adjoint form of the forward time-evolution operator 
.
Transient Growth in Fluid Flow
In the context of fluid flow problems, the dimension of our operator is much greater than that in the example above. A typical discretisation of a fluid flow problem has many thousands of data points. Analogously, an eigenvector in such a problem can be seen as some (localised) structure in the flow.
Publications
- C.D.Cantwell, D.Barkley, H.M.Blackburn, Transient growth analysis of flow through a sudden expansion in a circular pipe, Physics of Fluids 22 (34101), 2010.
- C.D.Cantwell, D.Barkley, Computational study of subcritical response in flow past a circular cylinder, Physical Review E 82 (26315), 2010.
- C.D.Cantwell, Transient growth of separated flows, PhD thesis, 2009